The Kelly Criterion formula calculates the potential sizes of wagers or investments that are the most likely to maximize the possible return while minimizing the risk of losses. This, coupled with the systematic way the formula handles bankroll management, the Kelly Criterion has been one of the top strategies used by investors, bettors, and traders for decades.
John L. Kelly Jr. developed the system in 1956 to try and ascertain what percentage of a bankroll should be wagered or invested based on the perceived odds. Understanding how it works and the applications that can be derived from it will give you greater security in making decisions where uncertainty and risk come into play.
What is the Kelly Criterion?
The Kelly Criterion formula is as follows:
f∗ = bp−q / b
Where:
- f∗ is the fraction of the bankroll to bet or invest.
- b is the odds received on the bet (i.e., the net odds minus 1).
- p is the probability of winning.
- q is the probability of losing (which is 1− p).
It’s the formula that gives the best fraction of bankroll to bet, given there’s a trade-off in growth and not losing too much at one go. If the formula returns positive, then the fraction of bankroll you should wager; if it is negative, it suggests don’t bet, since EV is not advantageous.
How the Kelly Criterion Works
The Kelly Criterion is used for maximizing the growth rate of capital over time, having in mind the proportion of bankroll to be risked in each bet or investment. It takes into consideration neither over-betting, which can perhaps lead to great losses, nor under-betting, where suboptimal growth will be attained.
Example of the Kelly Criterion in Betting
Suppose you are betting on a sports event with the following characteristics:
- The odds of your bet are 3.00 (which means you receive $3 for every $1 wagered, including your stake).
- You estimate the probability of winning (p) at 50%.
- The probability of losing (q) is, therefore, 50%.
Using the Kelly Criterion formula:
f∗=3×0.5−0.53−1f* = \frac{3 \times 0.5 – 0.5}{3 – 1}f∗=3−13×0.5−0.5
f∗=1.5−0.52f* = \frac{1.5 – 0.5}{2}f∗=21.5−0.5
f∗=12=0.5f* = \frac{1}{2} = 0.5f∗=21=0.5
Since the Kelly Criterion suggests that you wager 50% of your betting funds on this bet, if you have a $1,000 bankroll, the optimal bet size would then be $500. This approach allows you to maximize your potential growth while maintaining a buffer against potentially significant losses.

Conditional Factors and Assumptions
Several key factors and assumptions influence the application of the Kelly Criterion:
- Accurate Probability Estimates
The accuracy of the Kelly Criterion depends on the ability to have reasonably correct estimates for the probability of winning ‘p.’ Incorrect estimates result in a miscalculation that leads to over- or under-betting. This can include, in gambling, an understanding of the true odds of an event, which may be hard to estimate correctly. - Constant Odds
The Kelly Criterion assumes that the odds and probability will stay the same throughout. In the real world, these may shift based on new information or market variations. Refreshing the inputs into the formula-whenever new data becomes available is really important to keep the formula working well. - Divisibility of Bankroll
The formula assumes that the bankroll can be divided into smaller units and that it is possible to bet fractional amounts. This can be impractical in certain betting scenarios where minimum bet sizes are imposed or in markets where liquidity is an issue. - Risk Tolerance
The Kelly Criterion seeks growth maximization, but it does not take into consideration another factor that is just as important: individual risk tolerance. Some people may want to wager less than the Kelly amount to minimize variance and prevent losing streaks.
Over-Betting and Under-Betting
- Over-Betting:
This occurs when a bettor wagers too large a portion of their bankroll, increasing the risk of ruin. For instance, betting more than the Kelly fraction can lead to significant losses, even with a positive expected value. - Under-Betting:
Betting less than the Kelly fraction results in slower growth. While it reduces risk, it also means that potential profits are not maximized. Some bettors opt for a “fractional Kelly” strategy, betting a smaller fraction, such as half or quarter Kelly, to balance growth with reduced risk.
Application Beyond Betting
The Kelly Criterion is far from a gambling-only solution and finds extensive applications in both finance and investment. For instance, in stock trading, it may answer such questions as how much capital one needs to invest in a certain stock or asset, given the expected return and volatility. Again, the aim is to maximize portfolio growth with a minimum chance of significant losses.
Example in Investing
An investor believes a particular stock has a 60% chance of making a 20% return and a 40% chance of losing 10%.
The Kelly Criterion system suggests investing 40% of the available capital in this stock; this approach helps the investor allocate their resources so they can maximize growth while accounting for the associated risk. To apply the Kelly Criterion:
- p=0.6p = 0.6p=0.6
- q=0.4q = 0.4q=0.4
- Expected return = 20% (or 0.20)
- Loss = 10% (or -0.10)
The formula becomes:
f∗=(0.20×0.6)−(0.10×0.4)0.20f* = \frac{(0.20 \times 0.6) – (0.10 \times 0.4)}{0.20}f∗=0.20(0.20×0.6)−(0.10×0.4)
f∗=0.12−0.040.20f* = \frac{0.12 – 0.04}{0.20}f∗=0.200.12−0.04
f∗=0.080.20=0.4f* = \frac{0.08}{0.20} = 0.4f∗=0.200.08=0.4
The Kelly Criterion suggests investing 40% of the available capital in this stock. This approach helps the investor to allocate their resources in a way that maximizes growth while accounting for the associated risk.

Limitations of the Kelly Criterion
Despite its benefits, the Kelly Criterion has limitations that must be considered:
- Sensitivity to Input Errors: The formula relies on accurate estimates of probability and odds. Small errors in these estimates can lead to significantly different bet sizes.
- Volatility: Following the Kelly Criterion exactly can lead to high volatility in returns, especially when bet sizes are large. To mitigate this concern, many bettors use a fractional Kelly approach, a modification of the original Kelly Criterion system.
Practical Constraints: In real-world scenarios, factors such as liquidity, transaction costs, and position size limits can restrict the application of the Kelly Criterion.
Conclusion
The Kelly Criterion offers a straightforward and mathematical strategy for choosing the size of a bet in uncertain circumstances to maximize the potential for long-term capital growth. It’s an analytical way of valuing a wager, balancing potential gains against the possibility of devastating losses.
This requires a certain degree of probability estimation and, if the criterion were to be effectively used, acceptance of its innate volatility. The Kelly Criterion is of value where decision-making needs to be linked to risk in a wide range of fields, from gambling to investment and trading.
What is the Kelly Criterion method?
The Kelly Criterion is a mathematical formula used to determine the optimal size of a bet in order to maximize the long-term growth of your bankroll while minimizing the risk of losing it all. It was originally developed by John L. Kelly Jr. in 1956 to optimize bet sizing for gamblers and investors. The Kelly Criterion is widely used in poker, sports betting, and investing to find a balance between risk and reward.
Formula:
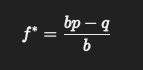
Where:
- f∗f^*f∗ is the fraction of your bankroll to bet.
- bbb is the odds you are getting on the bet (i.e., how much you win relative to your stake).
- ppp is the probability of winning the bet.
- qqq is the probability of losing the bet, which is equal to 1−p1 – p1−p.
Key Concepts:
Optimal Bet Size:
The Kelly Criterion tells you the ideal proportion of your bankroll to bet on each wager. It seeks to maximize the logarithmic growth of your bankroll by taking into account the probability of winning and the odds you are offered.Maximizing Long-Term Growth:
The idea behind the Kelly Criterion is that by betting a fraction of your bankroll based on the formula, you will grow your bankroll at the fastest rate over time, avoiding both the risk of ruin (losing your entire bankroll) and the underperformance of betting too conservatively.Risk-Reward Balance:
The Kelly Criterion offers a balance between betting too much (which can lead to significant losses) and betting too little (which can limit potential growth). By calculating the optimal bet size based on odds and probabilities, it aims to maximize your long-term return.
Example:
Let’s say you are in a poker game where you have a 60% chance of winning a pot and the pot will pay 2:1 (you win two dollars for every one dollar you bet).
- p=0.60p = 0.60p=0.60 (60% chance of winning)
- q=1−0.60=0.40q = 1 – 0.60 = 0.40q=1−0.60=0.40 (40% chance of losing)
- b=2b = 2b=2 (you win two times your bet)
Using the Kelly Criterion formula:

So, according to the Kelly Criterion, you should bet 40% of your bankroll on this hand.
Advantages of the Kelly Criterion:
Maximizes Bankroll Growth: By using the Kelly Criterion, you can achieve the highest possible rate of return on your bankroll in the long run, as it accounts for both winning probabilities and payout odds.
Prevents Ruin: The formula helps prevent the risk of going broke by never betting too much relative to your bankroll, even in situations with high potential rewards.
Optimizes Risk: The Kelly Criterion helps find the ideal balance between risk and reward, providing an effective strategy for maximizing profits without taking on excessive risk.
Disadvantages of the Kelly Criterion:
Requires Accurate Probabilities: The formula relies on knowing the exact probability of winning and the odds offered, which may not always be easy to determine, especially in dynamic environments like poker.
Volatility: While the Kelly Criterion is designed to maximize long-term growth, it can lead to large fluctuations in the short term. A player betting the full Kelly amount may experience periods of high volatility, even if the long-term results are positive.
Fractional Kelly: Some players use a fractional Kelly strategy, where they bet a fraction of the optimal amount suggested by the Kelly Criterion (e.g., half-Kelly or quarter-Kelly) to reduce the volatility. This allows for slower, more conservative bankroll growth.
Conclusion:
The Kelly Criterion is a powerful method for determining optimal bet sizes, balancing risk and reward in a way that aims to maximize the long-term growth of your bankroll. While it offers many benefits, particularly in terms of bankroll management, it requires accurate knowledge of odds and probabilities to be effective. By understanding and applying this formula, players can make more informed decisions about how much of their bankroll to risk in each bet.
What are the assumptions of Kelly criterion?
The Kelly Criterion relies on a set of assumptions to ensure its effectiveness in optimizing bet sizes and maximizing long-term bankroll growth. These assumptions are critical for applying the formula accurately and achieving the desired results. Below are the primary assumptions of the Kelly Criterion:
1. Accurate Probability Estimates
- The Kelly Criterion assumes you have precise and reliable estimates of the probability of winning (ppp) and losing (q=1−pq = 1 – pq=1−p) for any given bet.
- If these probabilities are inaccurate or miscalculated, the Kelly formula can suggest suboptimal or even harmful bet sizes.
- Example: In poker, you need to know your equity (your chances of winning a hand) to determine the correct bet size.
2. Known Payoff (Odds)
- The Kelly Criterion assumes that the odds (bbb) or the payout ratio of the bet are known and fixed.
- In practical terms, this means you must know how much you stand to win relative to your stake.
- If the odds change mid-bet or are miscalculated, the suggested Kelly bet size may no longer be optimal.
3. Bankroll is Divisible and Flexible
- The formula assumes your bankroll can be infinitely divided, allowing you to bet precise fractions of it (e.g., 12.5%).
- In real life, particularly in poker or gambling, bet sizes are often limited by minimum or maximum stakes, which can prevent strict adherence to the Kelly bet size.
- Additionally, your bankroll must be “flexible,” meaning you can adjust bet sizes dynamically as your bankroll grows or shrinks.
4. No External Constraints
- The Kelly Criterion assumes there are no external constraints on the size of your bet. This means:
- There are no table limits or betting caps that restrict the amount you can bet.
- You always have access to your full bankroll and can allocate it freely.
- In poker or sports betting, practical constraints (like table stakes) may limit how much of your bankroll you can bet.
5. No Correlation Between Bets
- The Kelly Criterion assumes that bets are independent of one another. The outcome of one bet does not influence the probability of success for the next.
- If bets are correlated (e.g., one poker hand affecting future play), this can impact the formula’s effectiveness.
- Example: In multi-street poker games, decisions on one betting round affect the outcome of future streets, which complicates applying the Kelly formula directly.
6. Long-Term Focus
- The Kelly Criterion assumes you are focused on long-term bankroll growth, not short-term fluctuations.
- While it maximizes long-term growth, the Kelly strategy can produce significant short-term volatility, which may not suit risk-averse players.
- Players who prioritize avoiding large swings might adopt a fractional Kelly strategy, betting a smaller percentage of the suggested Kelly amount.
7. Risk of Ruin is Avoided
- The Kelly Criterion assumes you will not go broke as long as you strictly follow the suggested bet sizes.
- However, if you overestimate probabilities or deviate from the Kelly bet, you increase the risk of bankroll ruin.
8. Single Bet at a Time
- The formula assumes you place one bet at a time and can adjust your bankroll before placing the next bet.
- In reality, poker tournaments or multi-bet scenarios can involve simultaneous risks, which complicates Kelly-based decisions.
Summary of Assumptions:
| Assumption | Description |
|---|---|
| Accurate Probabilities | You know the exact probability of winning and losing. |
| Known Payoffs (Fixed Odds) | The payout or odds are fixed and do not change mid-bet. |
| Divisible Bankroll | Your bankroll can be divided into precise fractions. |
| No Betting Constraints | No table stakes, caps, or limits restricting your bet size. |
| Independent Bets | Outcomes of bets are independent of each other. |
| Long-Term Focus | The goal is to maximize long-term bankroll growth. |
| Avoiding Ruin | Bet sizes suggested by Kelly prevent losing your entire bankroll. |
| Single Bet Per Calculation | You place one bet at a time, adjusting after each outcome. |
Practical Implications:
While the Kelly Criterion is mathematically sound, in practice, the assumptions are often challenging to meet. For poker players, odds and probabilities can change dynamically, bets are often correlated across streets, and bankrolls are subject to constraints. To address these challenges, many players use fractional Kelly betting (e.g., half-Kelly) to reduce short-term volatility and adjust for uncertainty in their estimates.
Understanding these assumptions is crucial for applying the Kelly Criterion effectively and ensuring that its strengths align with your bankroll management strategy.
What is the Kelly Criterion win loss ratio?
The best seat position in poker is generally considered to be late position, particularly the button (also known as the dealer button). Here’s why:
Advantages of Late Position:
More Information:
Being in late position means you act after most players have already made their decisions. This gives you valuable information about how they are playing the hand, allowing you to make more informed decisions based on their actions.Control of the Pot:
Players in late position have the ability to control the betting pace. You can choose to bet, check, raise, or fold based on what the other players do. This allows you to dictate the flow of the hand.Bluffing Opportunities:
Because you have the advantage of seeing your opponents’ actions before you have to make a decision, you can more easily spot weaknesses and use bluffs to take down pots.More Flexibility:
Late position gives you more options when it comes to hand selection. You can play a wider range of hands compared to early position, as you can evaluate how the other players act and adjust your strategy accordingly.
The Button (Dealer Position):
- Acting Last: The button is the last to act in every betting round except the first, giving you the maximum amount of information before making a decision.
- Position of Power: It’s often considered the most powerful seat in poker, as you can make decisions based on the actions of others, allowing you to play a more calculated and strategic game.
The Cutoff:
- The cutoff is the second-best position, acting right before the button. While not as strong as the button, it still provides an advantage, as you act after most players and can make strategic moves like stealing blinds or setting up bluffs.
Conclusion:
While the button is typically the most advantageous seat, late position overall is the best because it gives you more information and greater control over the hand. This allows you to make more profitable decisions, whether you’re playing a strong hand, bluffing, or trying to control the size of the pot.
What does it mean to play in position?
To play in position in poker means that you are acting later in the betting rounds compared to your opponents. This gives you the advantage of seeing how other players behave before making your decision, allowing you to make more informed choices based on their actions.
Advantages of Playing in Position:
More Information:
When you’re in position, you can observe how your opponents act before you make your decision. If they check, bet, or raise, you can adjust your strategy accordingly. This additional information can help you make better decisions about whether to bet, raise, call, or fold.Control Over the Pot:
Being in position allows you to control the flow of the hand more effectively. You can choose to bet, check, or raise based on the actions of others, which gives you more flexibility in how you approach the pot. This is especially valuable if you have a strong hand or want to control the size of the pot with a weaker hand.Bluffing Opportunities:
Players in position have more opportunities to bluff because they get to see how their opponents act first. If an opponent shows weakness (e.g., by checking), you can capitalize on that by making a well-timed bet or raise, increasing your chances of forcing them to fold.Better Pot Control:
Playing in position allows you to control the size of the pot more effectively. If you have a marginal hand, you can check behind to keep the pot small and avoid making a big commitment. On the other hand, if you have a strong hand, you can size your bets to build the pot and extract more value.
Example of Playing in Position:
Let’s say you’re in the cutoff (late position), and the player in the small blind raises. You can see how they act before you decide whether to call, raise, or fold. If the small blind has made a weak bet or raised with a questionable hand, you can exploit this by re-raising (a “3-bet”) to take control of the hand. Alternatively, if the small blind checks, you might choose to bet or check behind to see the next card.
Conclusion:
Playing in position is a key concept in poker because it allows you to make more informed decisions based on how your opponents act. By acting later in the round, you have the ability to control the pot, bluff more effectively, and make more profitable decisions overall. This is why players often seek to play in position whenever possible, especially in no-limit cash games and tournaments.
What is the gun position in poker?
In poker, the Under the Gun (UTG) position refers to the player who is seated immediately to the left of the big blind and is the first to act during the betting round, after the cards are dealt. Being in the UTG position is considered one of the most challenging positions because you must make a decision without having any information about how the other players will act.
Characteristics of the UTG Position:
First to Act: The player in the UTG position is the first to place a bet or make a decision (unless the action is passed to them after a check). This lack of information from other players makes it more difficult to play hands optimally.
Limited Information: Since no one else has acted yet, you’re making decisions without knowing how your opponents will respond, which can be risky, especially when you’re holding marginal hands.
Strategy for Playing UTG:
Because you are acting first, it’s important to play tighter and more conservative from the UTG position. The ideal strategy is to only play strong hands that have a good chance of holding up against potential raises from other players. These strong hands typically include premium hands like:
- Pocket Aces (AA)
- Pocket Kings (KK)
- Ace-King (AK)
- Pocket Queens (QQ)
- Ace-Queen (AQ)
Playing weak hands from UTG can often lead to difficult decisions and significant losses because you won’t have the advantage of seeing how the other players act before you have to make a move.
Example:
If you’re in the UTG position and you’re dealt 10♠ 10♥, you might consider raising to build the pot or to protect your hand against weaker hands. However, if you have 7♠ 5♠, a hand that has little potential, it’s better to fold to avoid putting money into the pot with a marginal hand.
Conclusion:
The UTG position is often regarded as one of the least favorable positions because you have to act with limited information. As a result, it’s best to play tighter and more conservatively from this seat, focusing on strong hands and avoiding risky moves.
What is the early position in poker?
In poker, early position (EP) refers to the seats located immediately to the left of the big blind and typically includes the Under the Gun (UTG) position and sometimes the UTG+1 seat. Players in early position are the first to act during the betting round, which means they have limited information about the actions of other players. This makes early position one of the most challenging places to play from, as you must make decisions without knowing how others will behave.
Characteristics of Early Position:
First to Act: Players in early position must make their decisions before seeing how the other players will act. This puts them at a disadvantage, as they lack information on whether opponents will raise, call, or fold.
Vulnerability: Since you have no idea how others will play their hands, you are more likely to face raises or re-raises when you play marginal hands, putting you at risk of losing chips or even your entire stack.
Tight Range: Given the disadvantages of acting early, players in early position should typically play a tighter range of hands. It’s recommended to only play premium hands that have a strong chance of winning, as you cannot afford to be caught in a difficult situation with a weak hand.
Recommended Hand Selection for Early Position:
Since you are acting first and don’t have any information from other players, it’s best to only play strong hands from early position. These are typically hands like:
- Pocket Aces (AA)
- Pocket Kings (KK)
- Ace-King (AK)
- Pocket Queens (QQ)
- Ace-Queen (AQ)
Hands that have a high likelihood of making strong post-flop hands, such as Ace-Jack (AJ) or Pocket Jacks (JJ), may also be playable depending on the situation.
Example:
- If you’re in the UTG position and you’re dealt A♠ K♠, you might raise to build the pot or make a value bet, as this is a strong hand.
- However, if you’re dealt 7♣ 4♠ in early position, it’s better to fold, as it’s a weak hand that can easily get you into trouble if you get involved with other players.
Strategy for Early Position:
- Be Selective: You should only play premium hands or hands with a strong chance of improving post-flop, such as suited connectors or high pocket pairs.
- Avoid Bluffing: Bluffing from early position can be risky, as you’ll have fewer opportunities to read your opponents and adjust your strategy. It’s usually safer to play hands that have inherent strength.
- Raise or Fold: In early position, you’re typically better off raising with a strong hand to build the pot or folding weaker hands to avoid unnecessary risk.
Final Thoughts
Early position in poker is a disadvantageous place to be because you’re forced to act without knowing how your opponents will behave. Therefore, playing tight and selectively is key. By only entering pots with strong hands, you can minimize the risks of being outplayed and make the most of the limited information available to you.
What is the strongest position in poker?
The strongest position in poker is typically considered to be late position, particularly the button (also known as the dealer button). This position offers significant advantages in terms of information, control over the pot, and flexibility in decision-making.
Reasons Why Late Position is the Strongest:
- In late position:
You act last in each betting round, which means you get to observe how the players before you act. This gives you a massive advantage because you can base your decisions on the actions of others, such as whether they check, bet, or raise. This allows you to make more informed and strategic decisions. - Control Over the Pot:
Players in late position, especially the button, have the ability to control the size of the pot. If you’re holding a strong hand, you can raise to build the pot. If you want to keep the pot small with a weaker hand, you can check or call. This flexibility can help you minimize losses and maximize gains. - Bluffing Opportunities:
Acting last allows you to bluff more effectively. You can identify weak players who might check or bet passively and use this information to your advantage by making a well-timed bluff. You also have the opportunity to raise if the earlier players are showing weakness, increasing your chances of stealing the pot. - Wider Range of Hands:
In late position, you can play a wider range of hands compared to earlier positions. Since you have more information on how others are betting, you can afford to take risks with marginal hands or speculative hands like suited connectors, low pocket pairs, or small suited aces. These hands might not be profitable from early or middle positions but can work well from late position due to the ability to see others’ actions first. - Easier to Steal Blinds:
From late position, especially on the button, you have the opportunity to steal the blinds by raising when the players in the blinds are weak or passive. This can be a profitable strategy in no-limit cash games and tournaments, especially in later stages.
The Button (Dealer Position):
The button is the most powerful position in poker. As the last player to act, the button allows you to:
- Decide the flow of the game: After observing how others act, you can decide to raise, call, or fold.
- Control the pot size: You can increase or decrease the pot size based on your hand strength.
- Capitalize on weak players: If opponents in early or middle positions are playing passively, you can exploit that by stealing the blinds or using a well-timed bet or bluff.
Final Thoughts
The button and late position are the strongest positions in poker because they offer the most information, control over the game, and opportunities to manipulate the pot. Playing from late position allows you to make more informed and strategic decisions, which can greatly improve your chances of success in the long run.
What is the late position in poker?
In poker, late position refers to the seats that act after most other players during a betting round, with the button (dealer button) being the last player to act. The advantage of being in late position is that you get to observe how your opponents behave before you make your decision. This allows you to make more informed choices based on the actions of the players before you.
Key Positions Within Late Position:
Cutoff (CO):
The player sitting immediately to the right of the button. The cutoff is the second-last to act in each betting round and is often considered the second-best position after the button.Button (Dealer Position):
The player sitting directly on the dealer button, who acts last in every betting round except the first one (pre-flop). This is generally considered the strongest position at the table, as the player can make decisions based on the actions of all the other players.
Advantages of Late Position:
More Information:
Being last to act means you have more information about the strength of other players’ hands. You can observe their betting patterns, allowing you to make more informed decisions about whether to bet, raise, call, or fold.Control Over the Pot:
Players in late position have the ability to control the size of the pot. You can decide to bet or raise if you believe your hand is strong, or you can check or fold if the situation suggests your opponents have better hands.Bluffing Opportunities:
Late position allows for more effective bluffing. If players before you check or make small bets, you can choose to raise or bluff to take control of the hand, knowing that you have the advantage of acting last.More Flexibility with Hand Selection:
In late position, you can play a wider range of hands. Since you’ve seen how the players before you have acted, you can take more risks with marginal hands like suited connectors, low pocket pairs, or weaker aces, which would typically be less playable in earlier positions.Stealing the Blinds:
If the players in the blinds (small blind and big blind) are weak or playing passively, you can raise to steal the blinds, especially when you’re in the cutoff or on the button. This is a common strategy in tournaments or cash games.
Example:
If you’re in the button position and the players in early or middle positions just call the big blind or check, you can raise with a wider range of hands, such as small suited connectors or weak aces. This would be riskier from an earlier position, but in late position, you have more leverage because you can see how the others act first.
Final Thoughts
Late position, especially the button and cutoff, is one of the most powerful positions in poker. The ability to make decisions after observing the actions of other players provides a significant strategic advantage, giving you control over the hand and more opportunities to make profitable plays, including stealing blinds, bluffing, or playing a wider range of hands.
What's the hardest position to play?
The hardest position to play in poker is generally considered to be early position, particularly the Under the Gun (UTG) position, which is the player seated immediately to the left of the big blind.
Reasons Why Early Position is the Hardest:
Limited Information:
In early position, you have to act before seeing how the other players will behave. This means you’re making decisions without any insight into whether your opponents will fold, call, or raise. As a result, you’re forced to play more conservatively because you have little information to guide your decisions.Vulnerability:
Players in early position are more likely to face raises or re-raises from players in later positions, putting them in tough spots. If you raise from early position with a weaker hand, you risk being challenged by players in later positions who have better hands, and you might face difficult decisions post-flop.Tighter Range:
To minimize risk, players in early position should play a very tight range of hands, typically only the strongest hands such as pocket pairs (Aces, Kings, Queens), Ace-King, and sometimes Ace-Queen. Playing weaker hands from early position can be risky because you’ll often have to play out of position on future streets, where the risk of losing increases.Lack of Control:
Since you’re acting first, you have limited control over the pace of the hand. Players in later positions can respond to your bet or raise, allowing them to dictate the flow of the game. You’re at a disadvantage because you can’t adjust your strategy based on how others are playing their hands.
Strategy for Early Position:
- Play Tight: To minimize risk, only enter pots with premium hands. You should avoid playing speculative hands (such as suited connectors or low pairs) that could put you in difficult situations post-flop.
- Raise with Strength: If you’re going to raise from early position, make sure it’s with a strong hand to ensure you’re not easily dominated by opponents who have a stronger hand or who can call with position.
- Avoid Bluffing Too Much: Bluffing from early position is generally not recommended because you have no information on how other players will act, and it’s difficult to get opponents to fold if you don’t have a strong hand yourself.
Final Thoughts
Early position is considered the hardest position to play because it requires a tight, conservative strategy with limited information. The lack of control over the pot and the difficulty of playing weaker hands effectively make it a challenging spot, especially in games with experienced players. By focusing on strong hands and playing more cautiously, you can minimize mistakes and avoid putting yourself in difficult situations.
What is the hijack position in poker?
In poker, the hijack position refers to the seat immediately to the right of the cutoff and two seats to the right of the button. It is one of the later positions at the table, but not as late as the cutoff or button. The hijack position is considered to be a “middle-late” position and can be a good spot to play from, as you have more information than players in early positions but less information than those on the button or in the cutoff.
Characteristics of the Hijack Position:
Acting Before the Button and Cutoff:
The hijack position acts after the players in early and middle positions but before the players in the cutoff and on the button. This gives you the advantage of seeing how many players have entered the pot, but you don’t have the advantage of acting last like players in the button or cutoff positions.More Flexibility in Hand Selection:
Since the hijack is closer to late position, you can play a wider range of hands compared to earlier positions. However, you still need to be mindful of the players behind you (especially in the cutoff and on the button), as they can raise or re-raise you with position.Stealing Blinds:
The hijack is a good position to attempt to steal the blinds (small blind and big blind) if the players in the blinds are passive or weak. This is particularly true if the table is playing tight, and you can raise with a wider range of hands to capitalize on your position.
Strategy for the Hijack:
Raise More Aggressively:
In the hijack, you can open your range a bit wider than from early positions. Hands like suited connectors, medium pocket pairs, and suited aces can be good candidates for raising or even folding, depending on the players in the blinds and their tendencies.Pay Attention to the Players Behind You:
The key consideration when raising from the hijack is the action of the players in the cutoff and on the button. These positions are stronger than the hijack, so you need to be cautious of their potential raises. If they are loose or aggressive, you might want to tighten your range, especially against players who are likely to re-raise.Steal the Blinds:
If the players in the blinds are tight or passive, you can try to steal the blinds with a wider range of hands. A raise from the hijack is often a good way to take advantage of weak players and accumulate chips without seeing a flop.
Example:
If you’re in the hijack position and you’re dealt K♠ Q♠, you might raise to steal the blinds or build the pot if you think the players behind you are likely to fold. However, if you’re holding 7♣ 3♠, it’s likely better to fold, as it’s a weak hand that can get you into trouble.
Conclusion:
The hijack position offers a balanced amount of flexibility and information. While it’s not as strong as the cutoff or button, it’s still a good spot to play hands aggressively, especially when trying to steal the blinds or build the pot with a strong hand. Players in the hijack should be aware of the positions behind them and adjust their strategy accordingly.



